声明
本节内容来源于 BiliBili视频数据结构与算法基础(青岛大学-王卓) 的 P89 - P93,本博客仅作笔记整理和学习记录,部分图片来自视频截图。
二叉树递归算法
先序遍历递归算法
1
2
3
4
5
6
7
8
| Status PreOrderTraverse(BiTree T){
if(T==NULL) return OK;
else{
visit(T);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
|
1
2
3
4
5
6
7
8
|
void Pre(BiTree *T){
if(T!=NULL){
printf("%d\t", T->data);
pre(T->lchild);
pre(T->rchild);
}
}
|
中序遍历递归算法
1
2
3
4
5
6
7
8
| Status InOrderTraverse(BiTree T){
if(T==NULL) return OK;
else{
InOrderTraverse(T->lchild);
visit(T);
InOrderTraverse(T->rchild);
}
}
|
后序遍历递归算法
1
2
3
4
5
6
7
8
| Status PostOrderTraverse(BiTree T){
if(T==NULL) return OK;
else{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
visit(T);
}
}
|
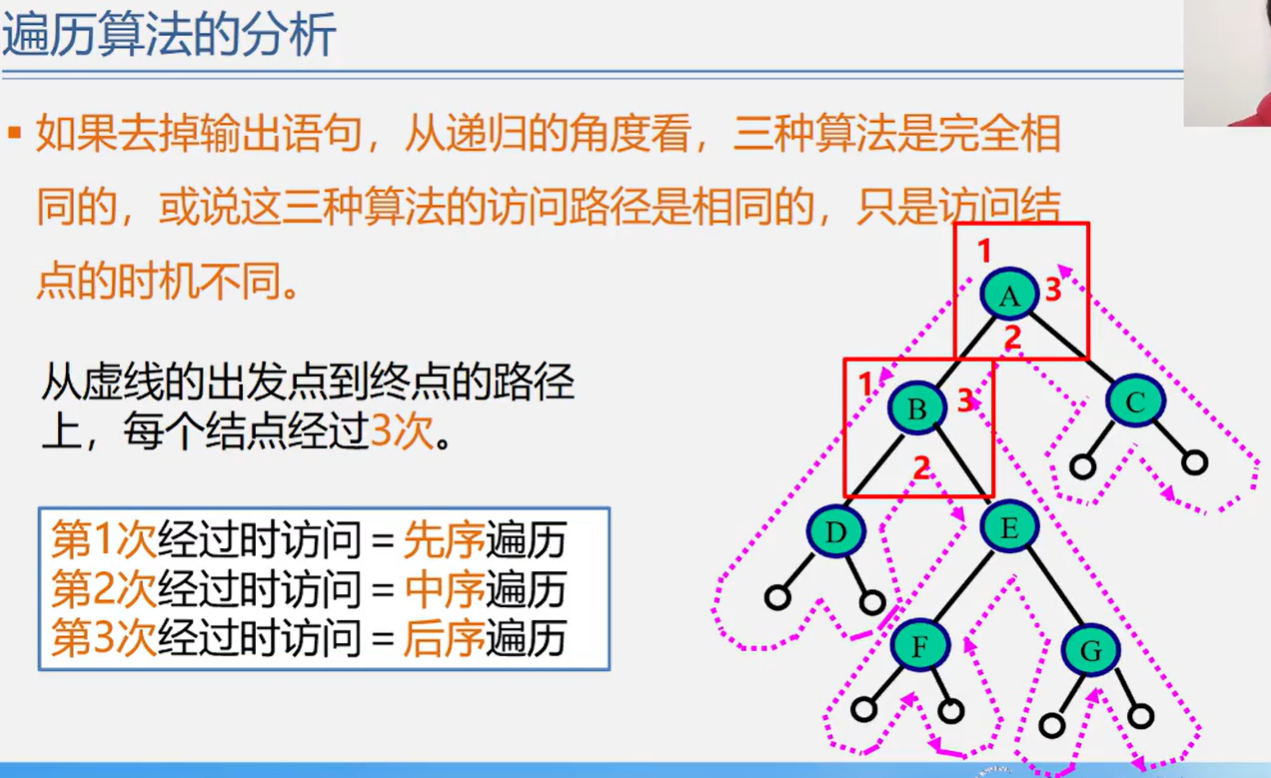
遍历算法的分析

时间效率: O(n)
空间效率: O(n)
二叉树非递归算法
中序遍历非递归算法
二叉树中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
- 建立一个栈
- 根结点进栈,遍历左子树
- 根结点出栈,输出根结点,遍历右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| Status InOrderTraverse(BiTree T){
BiTree p;
InitStack(S);
p=T;
while(p || !StackEmpty(S)){
if(p) {
Push(S,p);
p = p -> lchild;
}
else {
Pop(S,q);
printf("%c", q->data);
p = q -> rchild;
}
}
return OK;
}
|
二叉树层次遍历算法
算法设计思路:
使用一个队列:
- 将根结点进队;
- 队不空时循环:从队列中出列一个结点*p,访问它:
- 若它有左孩子结点,将左孩子结点进队;
- 若它有右孩子结点,将右孩子结点进队。
1
2
3
4
| typedef struct{
BTNode data[MaxSize];
int front, rear;
}SqQueue;
|
1
2
3
4
5
6
7
8
9
10
11
12
| void LecelOrder(BTNode *b){
BTNode *p;
SqQueue *qu;
InitQueue(qu);
enQueue(qu, b);
while(!QueueEmpty(qu)){
deQueue(qu, p);
printf("%c", p -> data);
if(p->lchild!=NULL) enQueue(qu, p->lchild);
if(p->rchild!=NULL) enQueue(qu, p->rchild);
}
}
|
二叉树遍历算法的应用(以先序遍历为例)
建立二叉树的二叉链表
1
2
3
4
5
6
7
8
9
10
11
| Status CreateBiTree(BiTree&T){
scanf(&ch);
if(ch== "#") T=NULL;
else{
if (!(T = (BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW);
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
return OK;
}
|
复制二叉树
算法思想:如果是空树,递归结束;否则,申请新结点空间,复制根结点递归复制左子树、递归复制右子树
1
2
3
4
5
6
7
8
9
10
11
12
| int Copy(BiTree T, BiTree &NewT){
if(T==NULL){
NewT = NULL;
return 0;
}
else{
NewT = new BiTNode;
NewT->data = T->data;
Copy(T->IChild, NewT->Ichild);
Copy(T->rChild, NewT->rchild);
}
}
|
计算二叉树的深度
算法思想:如果是空树,则深度为0;否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
1
2
3
4
5
6
7
8
9
| int Depth(BiTree T){
if(T==NULL) return 0;
else{
m = Depth(T->IChild);
n = Depth(T->rChild);
if(m>n) return (m+1);
else return(n+1);
}
}
|
计算二叉树的结点总数
算法思想:如果是空树,则节点个数为0;否则,节点个数为左子树的结点个数+右子树的结点个数再+1。
1
2
3
4
| int NodeCount(BiTree T){
if(T==NULL) return 0;
else return (NodeCount(T->lchild) + NodeCount(T->rchild) + 1);
}
|
计算二叉树的叶子节点总数
算法思想:如果是空树,则叶子节点个数为0;否则,节点个数为左子树的叶子结点个数+右子树的叶子结点个数。
1
2
3
4
5
| int LeadCount(BiTree T){
if(T==NULL) return 0;
if(T->lchild == NULL && T->rchild == NULL) return 1;
else return (LeadCount(T->lchild) + LeadCount(T->rchild));
}
|