声明
本节内容来源于 BiliBili视频数据结构与算法基础(青岛大学-王卓) 的 P76 - P80,本博客仅作笔记整理和学习记录,部分图片来自视频截图。
结点和节点的区别
- 节点是一个实体,它具有处理能力,比如网络上的一台计算机。
- 结点是一个交叉点、一个标记,算法中的点一般都称为结点,数据结构中的每一个数据元素都用中间标有元素值的方框来表示,我们称它为结点。
简单来说,节点是有功能的,而结点是有数据的。
树
树的特点
- 逻辑结构:非线性结构
- 常用于有层次的结构
- 一对多
树的定义
树(Tree)是 n(n≥0) 个结点的有限集。
若 n=0 ,称为空树;
若 n>0 ,有且仅有一个根(Root),可分为 m(m≥0) 个互不相交的有限集,其中每个集合本身又是一棵树,并称为根的子树(SubTree)。
- 树的定义是递归的定义。
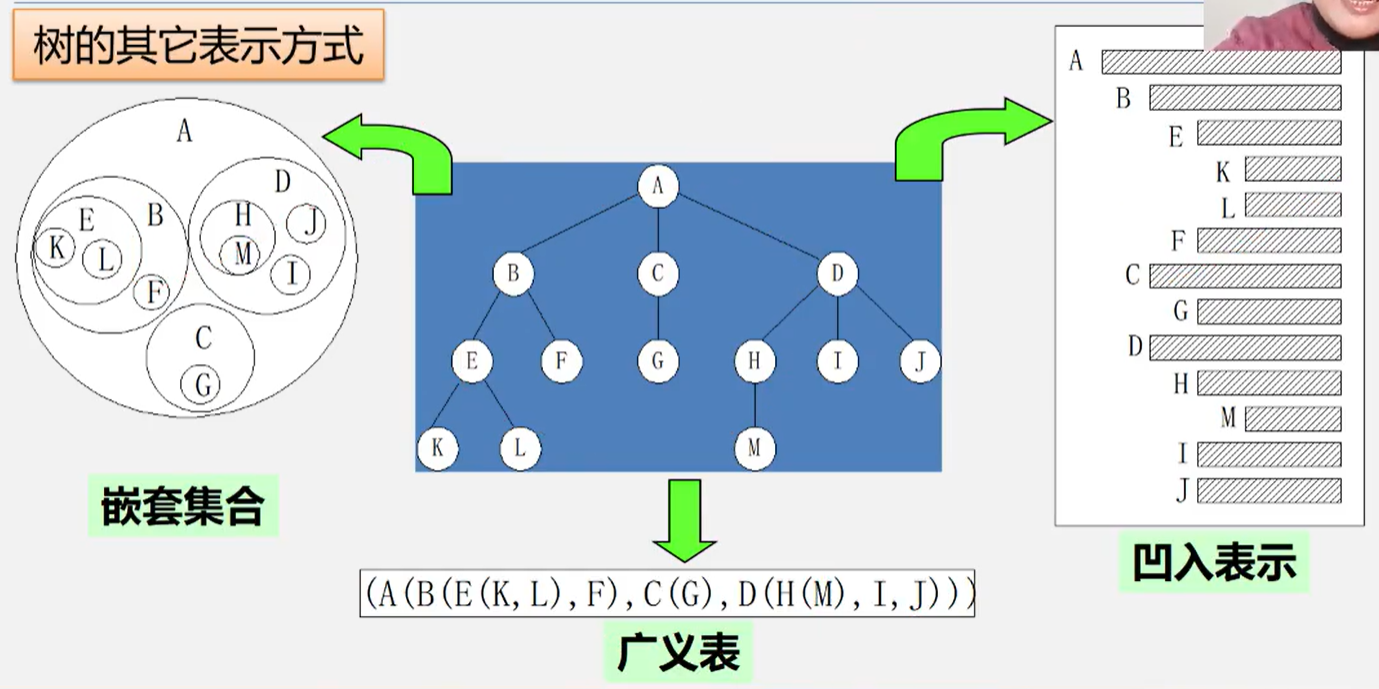
树的表示方式
- 示意图
- 嵌套集合
- 凹入表示
- 广义表
树的表示方法
树的基本术语
- 结点:数据元素以及指向子树的分支
- 根节点:非空树中无前驱结点的结点
- 节点的度:结点拥有的子树数
- 树的度:树内各结点的度的最大值
- 叶子(结点):终端结点(度 = 0)
- 分支结点:非终端结点(度 ≠ 0)
- 内部结点:根节点以外的分支结点
- 孩子和双亲:结点的子树的根成为该节点的孩子,该节点称为孩子的双亲
- 兄弟:有共同双亲的结点
- 堂兄弟:双亲在同一层的结点
- 结点的祖先:从根到该结点所经分支上的所有结点
- 树的深度:树中结点的最大层次
- 有序树:树中结点的各子树从左至右有次序(最左边的为第一个孩子)
- 无序树:树中结点的各子树无次序
- 森林:是 m(m≥0) 棵互不相交的树的集合
Tip:树一定是森林,森林不一定是树。
二叉树
为何要重点研究每结点最多只有两个“叉”的树?
- 二叉树的结构最简单,规律性最强;
- 可以证明,所有树都能转为唯一对应的二叉树,不失一般性。普通树(多叉树)若不转化为二叉树,则运算很难实现。
二叉树在树结构的应用中起着非常重要的作用,因为对二叉的许多操作算法简单,而任何树都可以与二叉树相互转换,这样就解决了树的存储结构及其运算中存在的复杂性。
二叉树的定义
二叉树是 n(n≥0) 个结点的有限集,它或者是空集 (n=0),或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。
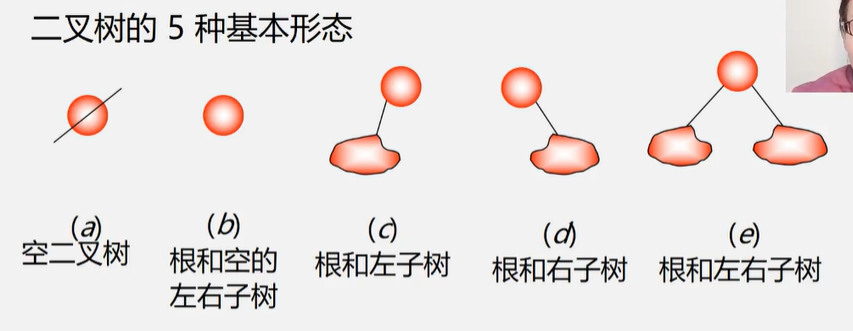
特点:
- 每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。
- 子树有左右之分,其次序不能颠倒。
- 二叉树可以是空集合,根可以有空的左子树或空的右子树。
Tip: 二叉树不是树的特殊情况
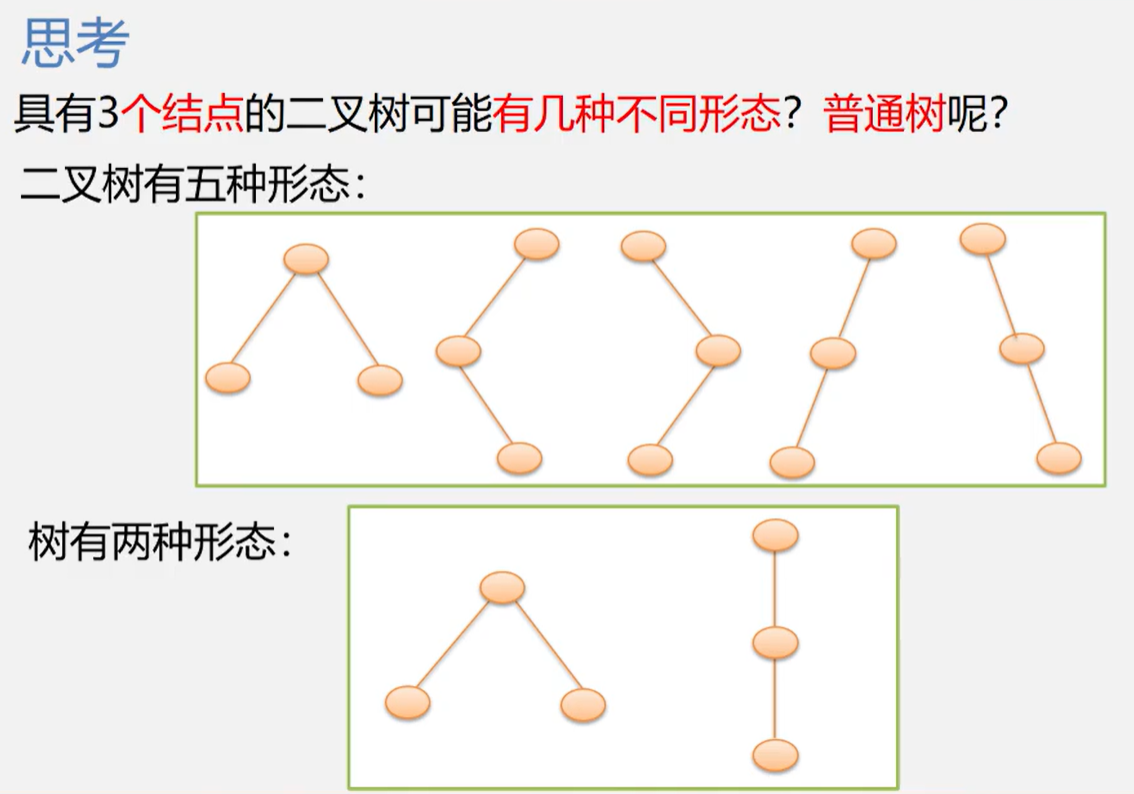
思考1
二叉树的五种基本形态
Tip:虽然二叉树与树概念不同,但有关树的基本术语对二叉树都适用。
二叉树的应用案例
- 数据压缩问题
- 利用二叉树求表达式的值
树和二叉树的抽象数据类型定义
二叉树中的重要操作:
c++
1 | CreateBiTree(&T,definition) |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 沐阳先生的博客!