声明
本节内容来源于 BiliBili视频数据结构与算法基础(青岛大学-王卓) 的 P86 - P88,本博客仅作笔记整理和学习记录,部分图片来自视频截图。
遍历二叉树
- 遍历定义:顺着某一条搜索路径巡访二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(又称周游)。
“访问”的含义很广,可以是对结点作各种处理,如:输出结点的信息、修改结点的数据值等,但要求这种访问不破坏原来的数据结构。 - 遍历目的:得到树中所有结点的一个线性排列。
- 遍历用途:它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
- 遍历方法:依次遍历二叉树中的三个组成部分,便是遍历了整个二叉树
遍历方法
假设: L:遍历左子树 D:访问根结点 R:遍历右子树
则遍历整个二叉树方案共有:DLR、LDR、 LRD、DRL、RDL、RLD 六种。
若规定先左后右,则有:
- DLR:先(根)序遍历
- LDR:中(根)序遍历
- LRD:后(根)序遍历
⭐用二叉树表示算数表达式
根据遍历序列确定二叉树
- 若二叉树中各结点的值均不相同,则二叉树结点的先序序列、中序序列和后序列都是唯一的。
- 由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一棵二叉树。
⭐已知二序列求二叉树
二叉树递归算法分析
二叉树的先序递归遍历算法
1 | Ststus PreOrderTraverse(BiTree T){ |
1 | //实现 |
二叉树的中序递归遍历算法
1 | Ststus InOrderTraverse(BiTree T){ |
二叉树的后序递归遍历算法
1 | Ststus PostOrderTraverse(BiTree T){ |
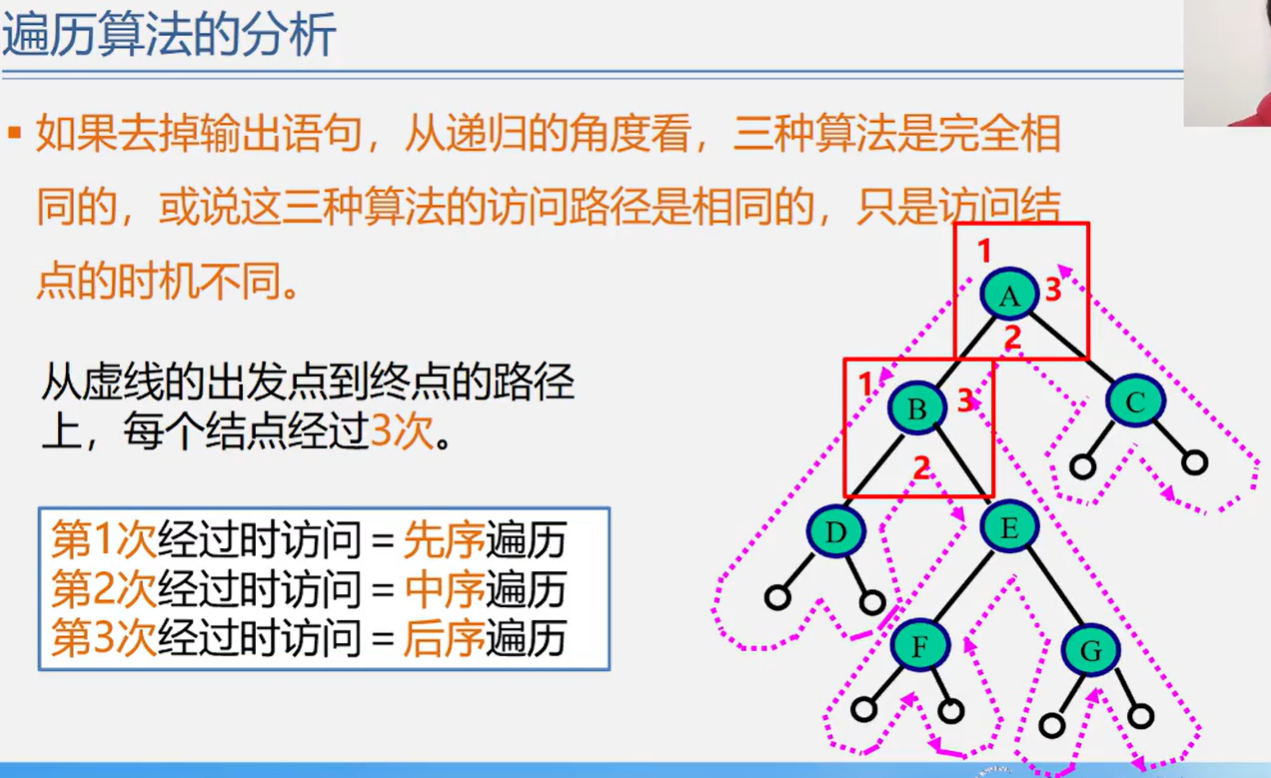
遍历算法的分析
时间效率: $ O(n) $
空间效率: $ O(n) $
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 沐阳先生的博客!
评论
TwikooGitalk